Pathfinding in 2D Platformers

Published on 25 Sep 2024

Table of Contents

• Introduction
• Discretising the Game World
• Building a Pathfinding Graph
  • Finding the Graph Nodes
  • Finding the Graph Edges
    • Node Reachability Example: Within a Single Platform
    • Representing Edges Meaningfully
    • Node Reachability Example: Jumping Between Platforms
    • Node Reachability Example: Using the Action List
  • Extending to Other Entities and Worlds
  • Accounting for Non-Discrete Positions
• Solving the Pathfinding Graph
  • Performance and Optimisations
• Conclusion
  • Further Reading

Introduction

Various pathfinding solutions exist for video games, with such solutions exhibiting different features and behaviours. A particular solution can be chosen intentionally depending on game design, rather than difficulty of implementation or efficiency; this post aims to give a technical description for how one can achieve accurate pathfinding in the context of a 2D platformer, but not whether the decision to do so is universally ‘right’ with respect to game design.

Discretising the Game World

Consider a typical 2D platformer scene:

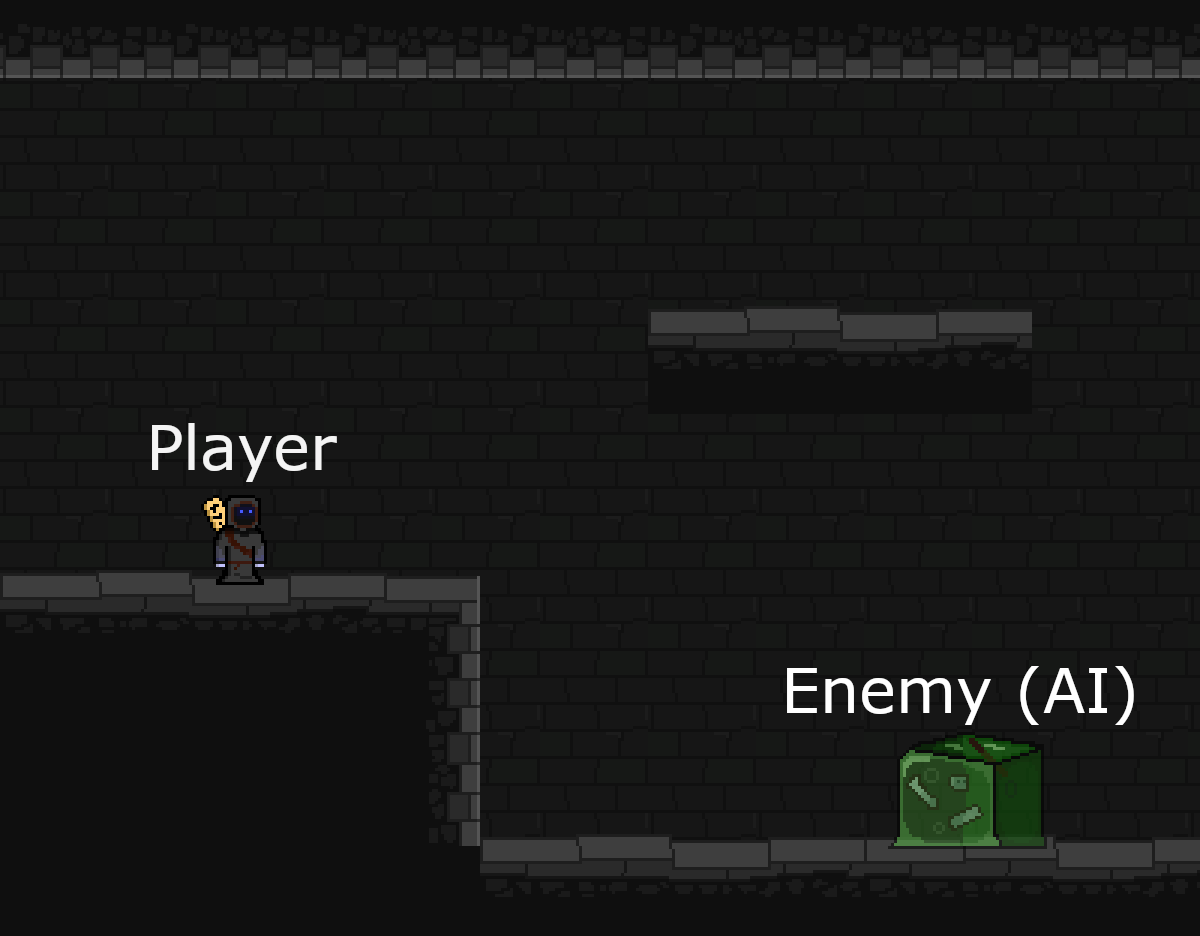
From here on, the word ‘entity’ will be used to describe the player or an enemy (or some other character) in the game.

Abstracting away the game’s art assets, the environmental setting can be viewed as a collection of collision shapes defined in 2D space (overlayed in blue):

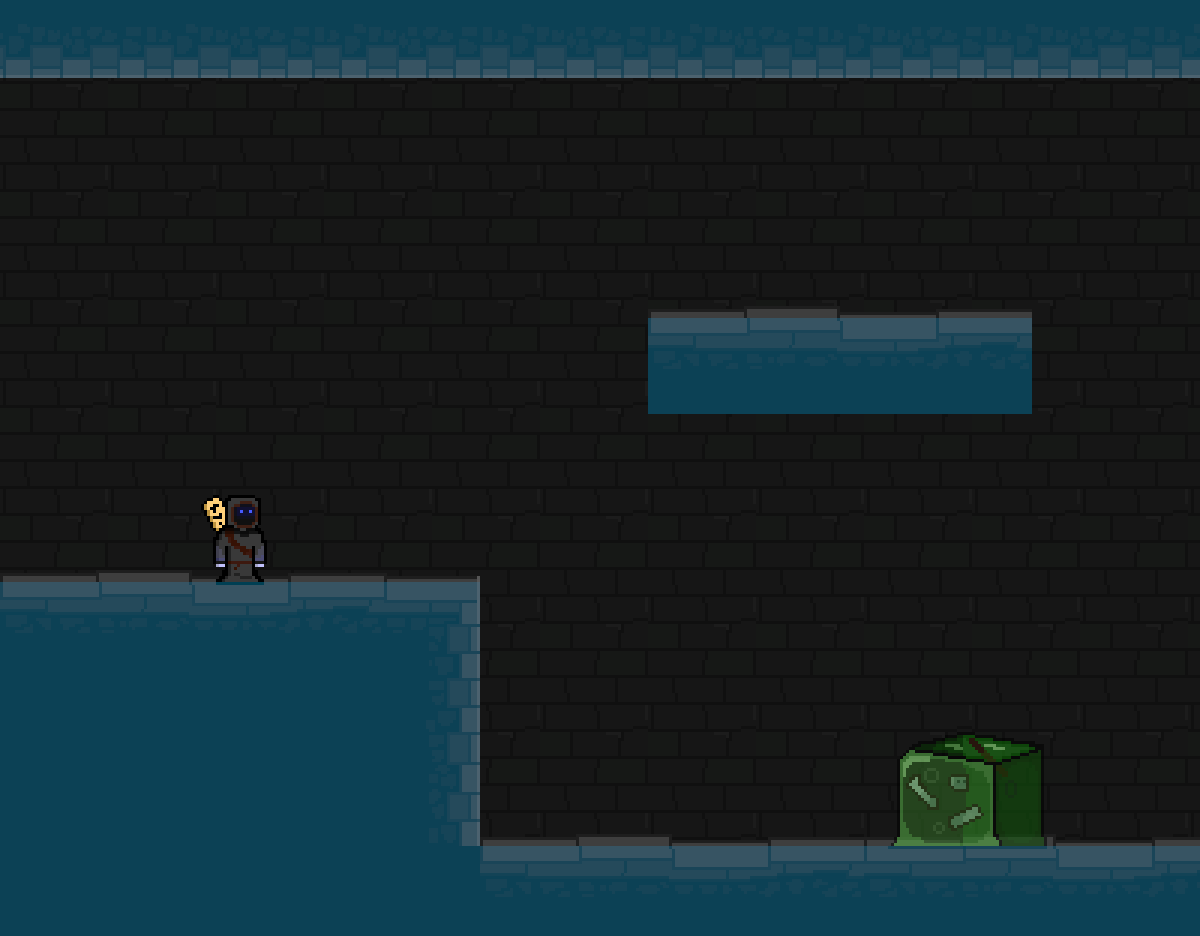
To make this world easier to process, it can be discretised into a grid of uniform segments. In practice, platformers are often designed with tilesets, so such a grid is already likely to be natural for a lot of game worlds.

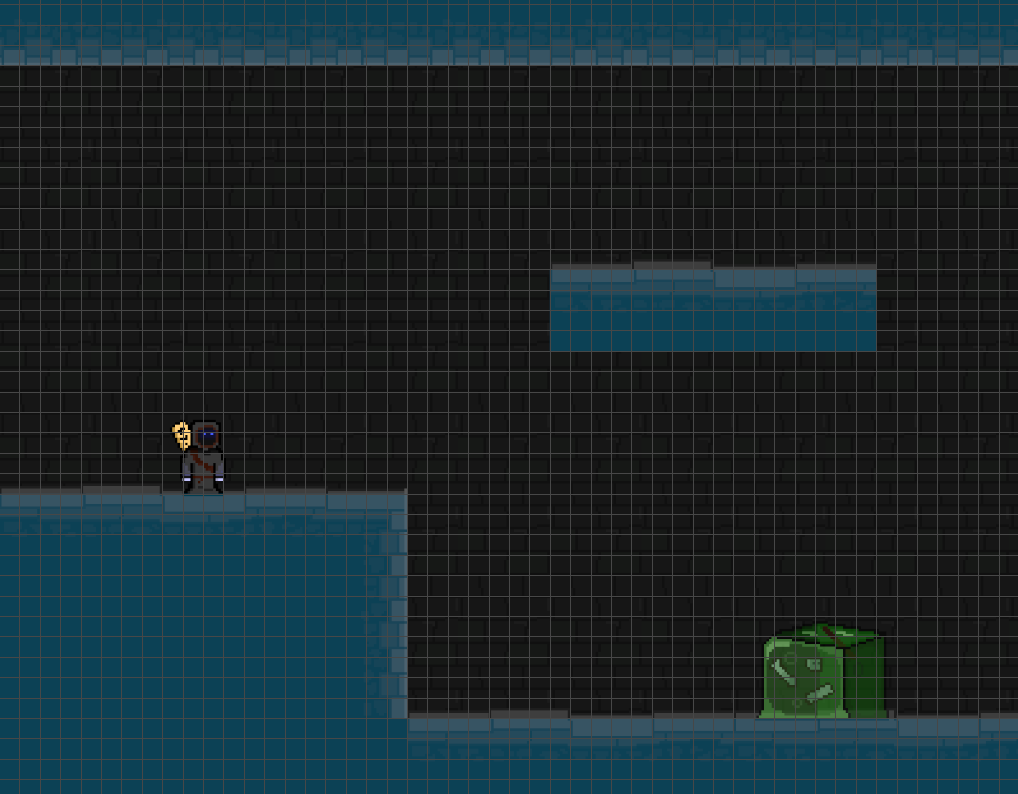
The side-length of each segment is somewhat arbitrary — for instance, in the example above, each segment could be subdivided into quarters, and each of those could be subdivided into quarters, and so-on. However, the smaller the segment length, the larger the graph will be (and thus the more memory and computational time is required to process it.) On the other hand, large segment lengths give the world less precision with which to build in, resulting in clunky-feeling levels and/or less natural pathing movement. I think a reasonable length is one which is at least smaller than the vast majority of entities in the game, but not significantly smaller than that. For the image above, the player character is approximately two segments wide, which I think is reasonable.

Building a Pathfinding Graph

Given an entity, the goal is now to take this discretization and to build a pathfinding graph, i.e. a graph which represents how an entity is able to move through the world.

For illustrative purposes, let us consider an entity which is affected by gravity, can move left and right, and can jump. This is essentially the basic moveset of Nintendo’s Mario character.

Finding the Graph Nodes

First, let us find all segments which are ‘walkable’, i.e. those which can be considered part of a ‘floor’/locations in which the entity can stand.

Let us first define an empty segment as any segment which has no environmental collision shape overlapping with it. For the image above, these are all segments that are not shaded in blue.

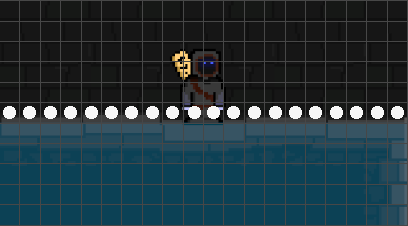
Then, let us define a walkable segment as any segment for which there is an empty segment directly above it, and a non-empty segment directly below it. Walkable segments are shown below as white circles:

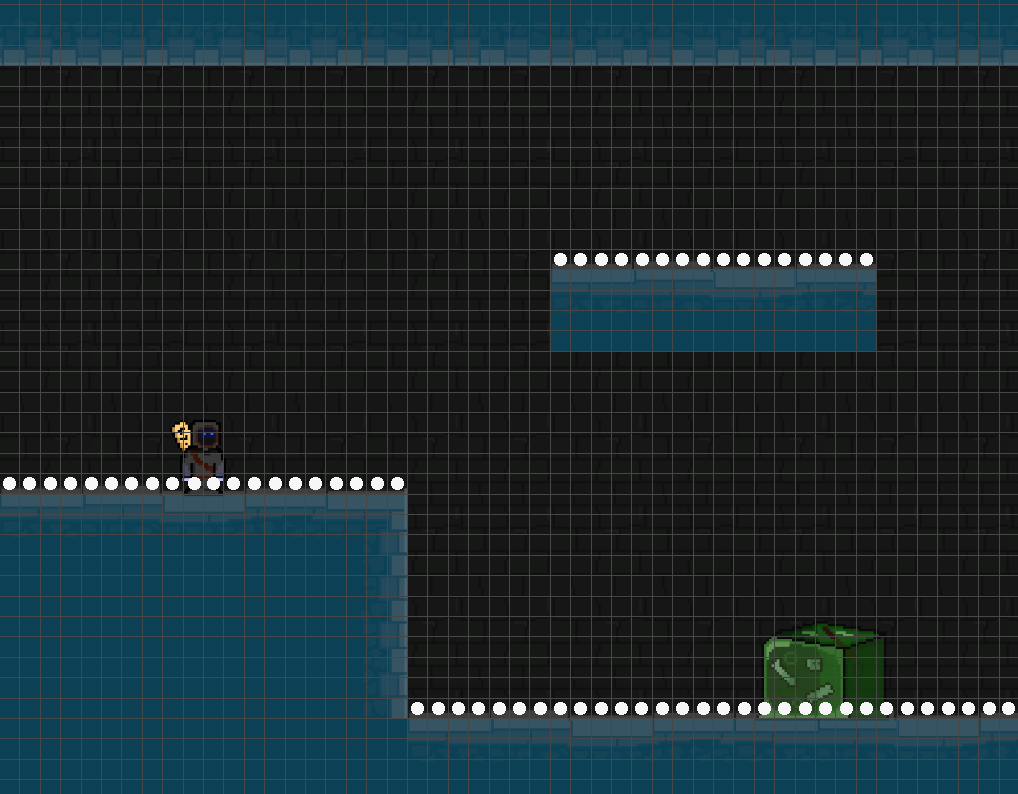
However, this is an intricacy to this approach — what’s ‘walkable’ to one entity might not be to a larger one. For instance, the ‘enormous slime’ on the upmost platform can be said to be colliding against the ceiling, so those segments should not be marked as ‘walkable’ for the particular ‘enormous slime’ entity:

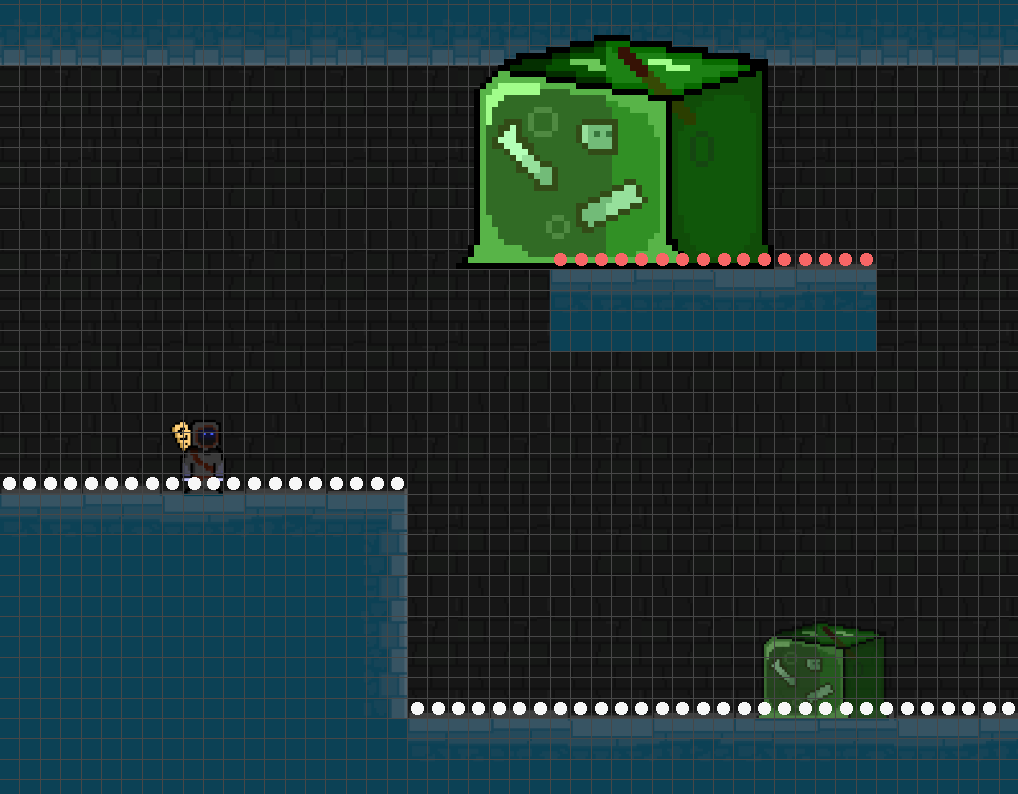
To account for this, the algorithm can be adjusted to consider entity sizes — for example, if considering the pathfinding graph of an entity with a height of 5 segments, then determining walkability of a particular segment should involve checking for 5 empty segments above a non-empty segment, instead of just 1.

After this process, every location in which the entity can stand has been found. These will form the node set of the pathfinding graph.

Finding the Graph Edges

Given the node set, the interconnectedness between nodes in that set can be investigated. Consider the function indicated by the signature:

In other words, getNodePairReachability takes a node which an entity is currently located at (src), a node which we are investigating the reachability of from src (dst) and returns an Edge object (described shortly) or null if reachability is not possible.

Fundamentally, if getNodePairReachability is called for every node pair in the graph, the pathfinding graph will be complete as the entire node set and edge set will have been found. Hence, let us look at how getNodePairReachability can work.

Node Reachability Example: Within a Single Platform

The most trivial case is when src and dst are directly and horizontally adjacent to one another — in such cases, the entity can simply move left or move right by one segment’s worth of distance.

We can extend this intuition to the general rule: For any two nodes with the same vertical coordinate, if there exist only walkable segments between those nodes, then they are neighbours in the pathfinding graph.

For example, consider the subgraph indicated by the following image:

Observe that for every node pair \((u,v)\) in this subgraph, \(u\) and \(v\) have the same vertical coordinate, and only walkable segments exist horizontally between \(u\) and \(v\). Therefore, every edge \((u,v)\) should be present in the edge set of the pathfinding graph, resulting in a complete digraph.

As an illustration, the image below depicts all edges outgoing from a particular source node (shown in green):

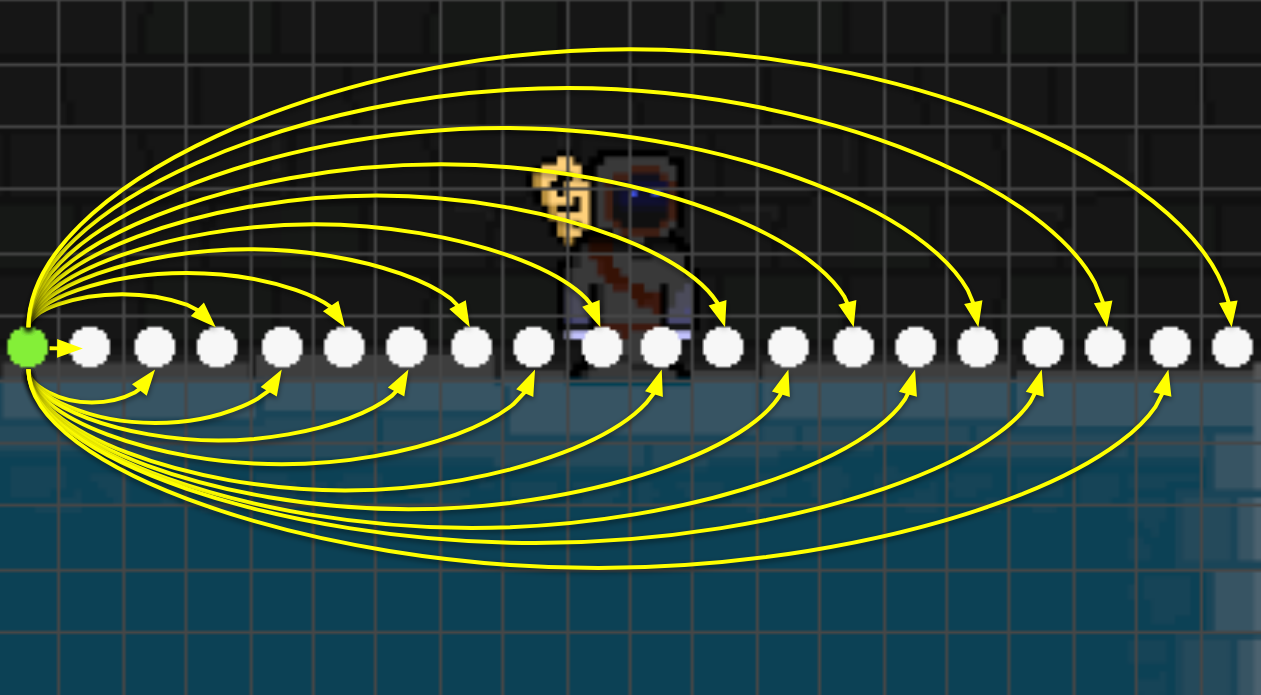
Representing Edges Meaningfully

Before continuing, let us describe how edges are represented usefully in the pathfinding graph. Each edge is represented by its own Edge object, but importantly, the Edge object does not just encode its two endpoints — it also consists of the action(s) that the entity needs to take to move from the source node to the destination node.

Each Action object represents a move in the entity’s moveset and a duration for how long to perform that move for. With regards to an idea of implementation for the Action structure, an enum (MovesetAction) could be used:

Continuing the discussion of the most trivial case, the direction of movement that the edge encodes can be easily found like so (where the source and destination nodes contain their pixel coordinates):

Determining the duration of the movement is less trivial, but one approach is by using using equations of motion. \[ \texttt{duration}\;:=\;\frac{\lvert \texttt{src.coords.x} - \texttt{dst.coords.x} \rvert}{\texttt{entity.horizontalSpeed}} \] where \(\texttt{entity.horizontalSpeed}\) is in pixels per second.

So at this point, we have a pathfinding graph which enables entities to horizontally pathfind across a single platform.

Node Reachability Example: Jumping Between Platforms

Having entities being only able to move across single platforms is quite limiting, and the technique used could be argued as quite over-engineered for that scope. However, one can also encode additional forms of node reachability based upon other moves available to the entity.

For example, consider a setting where there are two platforms (shown in blue) separated by a gap:

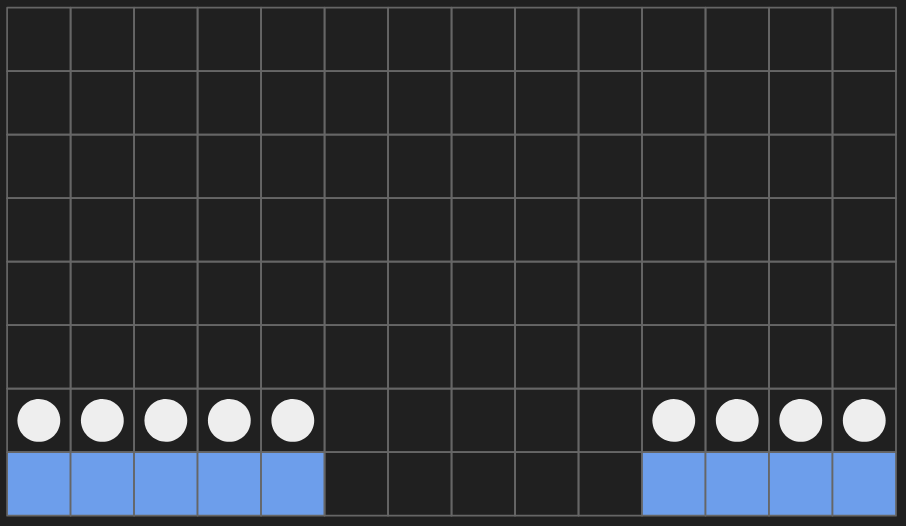
Again, walkable segments are shown by white circles.

Consider the reachability from the following source node (shown in green) to the destination node (shown in red):

Evidently, the entity can no longer simply move left or move right, as there are no walkable segments between the two nodes. However, recall that the entity is able to jump — therefore, it can instead be tested whether the destination is reachable from the source via the action of ‘simultaneously jumping and moving right’.

Using equations of motion and the pixel coordinates of the source and destination nodes, the distance that the entity would need to travel horizontally to reach the destination, \(d_{h}\) , can be found: \[ d_{h} := \lvert \texttt{src.coords.x} - \texttt{dst.coords.x} \rvert \] Then, the ‘airtime of the jump’, \(t_{\texttt{jump}}\) , can also be found, i.e. the length of time that the entity’s vertical coordinate stays above a particular value (normally the destination node’s vertical coordinate) after jumping. In this case, the destination node is at the same vertical coordinate as the source node, so: \[ t_{\texttt{jump}} := 2 \cdot t_{\texttt{apex}} \] where \(t_{\texttt{apex}}\) is the time taken for the entity to reach the top of their jump. Assuming that the entity starts with a vertical velocity of \(0\), has a ‘jump velocity’ \(v_{\texttt{jump}}\) (i.e. the vertical velocity given to the entity when they jump), and is under gravity \(g\) : \[ t_{\texttt{apex}} := \frac{v_{\texttt{jump}}}{g} \] Therefore: \[ t_{\texttt{jump}} := \frac{2 \cdot v_{\texttt{jump}}}{g} \] So, \(t_{\texttt{jump}}\) is exactly the amount of time that the entity has available to them to cover the horizontal distance \(d_{h}\) . Hence, the source node is connected to the destination node if: \[ t_{\texttt{jump}} \cdot \texttt{entity.horizontalSpeed} \geq d_{h} \] If this inequality holds, then an Edge can be added which encodes the action ‘simultaneously jump and move right’ for duration \(t_{\texttt{jump}}\) , e.g.:

Node Reachability Example: Using the Action List

When the Edge object was described, it was said to take a list of Action objects which the edge represents. However, the previous two examples result in only one action being needed to represent the edge, so I’d like to quickly give an example where it may be more natural to use a sequence of actions.

Note: The previous example could have theoretically used a sequence of actions, namely jumping for a duration of \(0\) (as the entity retains their velocity), and then moving right for a duration of \(t_{jump}\) .

Consider the following environment, where the colors denote the same meaning as before:

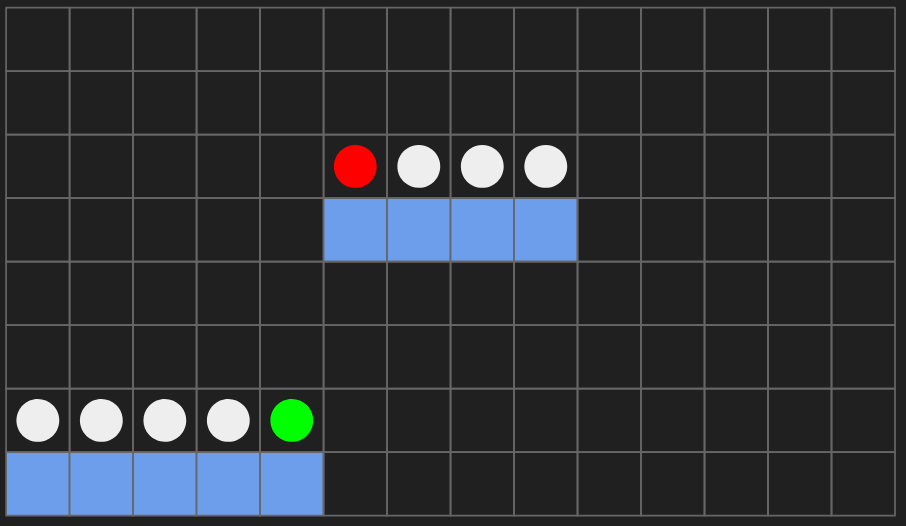
Observe how the previous action of ‘simultaneously jump and move right’ would no longer be likely to work, as it could result in the entity moving under the upper platform and thus colliding with its bottom, being unable to go on top of it.

Instead, a better strategy could be to jump until reaching the apex, and then moving right. This can be represented via a sequence of two actions — ‘jump’ (and wait to reach the apex) and then ‘move right’. Whether this edge exists can be found via similar reasoning to before, but critically, the edge is now represented as an ordered sequence of two actions.

Extending to Other Entities and Worlds

I hope that the examples given above are illustrative of how one can determine reachability between nodes in the graph. Importantly, these are just examples — depending on the game (namely the entities and environmental objects within that game) there can be huge variety in how edges are formed.

For instance, a game might contain a platform with one-way collision (i.e. one in which an entity can jump through it from below, and drop through it from above). This may require needing to identify which nodes of the graph are part of a droppable platform, and then testing for additional action sequence variants between that node and others.

Accounting for Non-Discrete Positions

At any timestep, a given entity might not be exactly at the coordinate represented by one of the segments, e.g. the purple circle below denotes where an entity could be ‘registered’ as being.

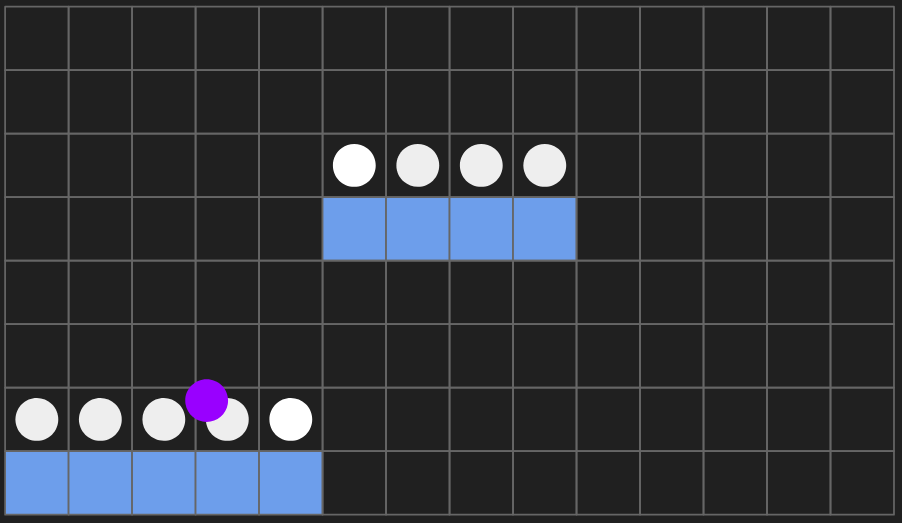
One option is to approximate the entity’s position to a segment (e.g. convert it to the nearest). However, this can result in less realistic behaviour.

Instead, a technique that I’ve found useful is to instantiate the entity’s position as a new node in the pathfinding graph, and to then use getNodePairReachability between it and surrounding nodes (essentially within some radius), and then continuing to find the shortest path in the graph (as described in the next section). Hence, it is important to have getNodePairReachability be as flexible and well-defined as possible.

Solving the Pathfinding Graph

Once we have the pathfinding graph, the problem is now essentially a shortest-path search from a source node (representing the entity’s position) to the destination node (typically representing the player’s position). The edge cost could (e.g.) be the Euclidean distance from its two endpoints, or the sum of the durations in the action sequence it holds (or a combination of both).

Typically, A* is the common algorithm for efficiently finding a path in this context. A good heuristic to start-off with is the Euclidean distance between the source node and the destination node, although note this is not necessarily an admissible heuristic if you’re considering durations in your edge cost.

Once the path has been found, the entity simply needs to execute the sequence of actions indicated by the edges of that path!

Performance and Optimisations

Solving to find the best route can be computationally intensive, even with a good heuristic, but there are some straightforward optimisations which can result in far more performant behaviour.

1. I recommend being wary of trying to perform all entity pathfinding within a single physics frame, as such computation is expensive. Instead, consider using multi-threading to background the task; this should not impact the player’s experience, as an entity does not need to have the updated shortest path every frame to be viewed as behaving realistically.

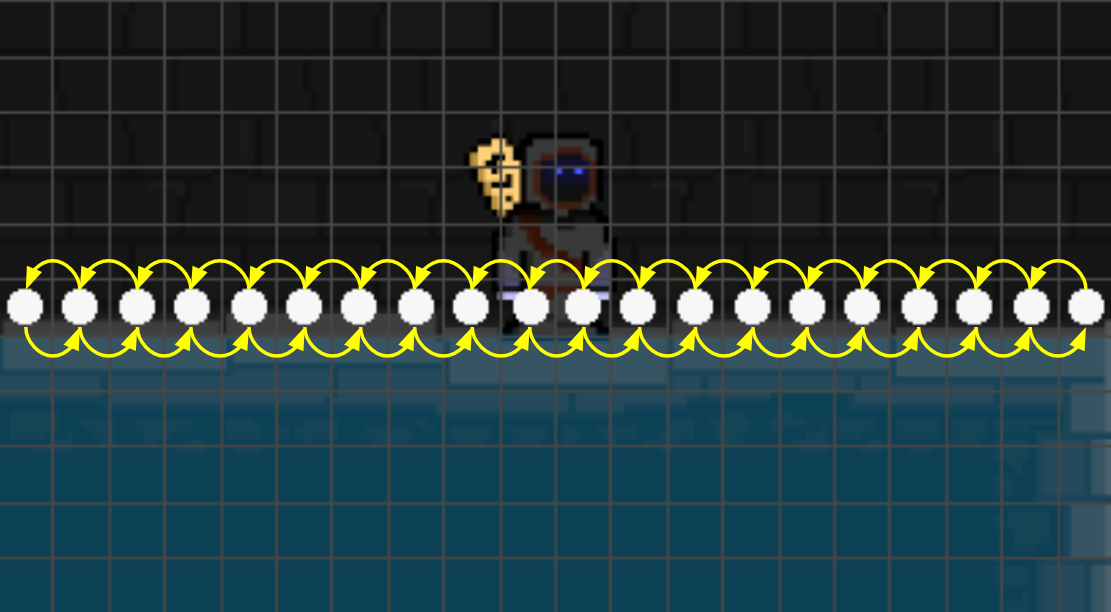
2. The getNodePairReachability described above creates a complete digraph for any platform-like subgraph, because every node of the platform has an edge to every other node of the platform. Hence, for \(n\)-many nodes in the subgraph, the number of edges is \(\mathcal{O}(n^{2})\).

   However, in-practice, one can remove all edges which are not between two directly adjacent nodes, as such edges can be composed by a sequence of directly adjacent edges. This reduces the number of edges to \(\mathcal{O}(n)\), resulting in a subgraph which looks like:

   

3. getNodePairReachability could return multiple edges for the same node pair, representing different sequences of actions. However, only one of these edges needs to be kept, and the rest (i.e. those with larger cost) should be immediately pruned.

4. If working with static worlds, then precompute the pathfinding graphs at compile-time. Similarly, if working with a chunk generation system, precompue the pathfinding graphs for each chunk, and then determine node reachability for adjacent chunks at runtime.

5. If working with a big world space, consider discretising the entire world into chunks of segments (e.g. one chunk could be \(200 \times 200\) segments). Then, if pathfinding between source nodes and destination nodes in different chunks, consider first computing the sequence of chunks which the entity should move through, and then only compute the path between the source node’s current chunk and the immediately-next chunk. This approach might not find the shortest path, but the returned path should be good enough to be reasonable.

Conclusion

I hope that this post has given some ideas on how to implement accurate pathfinding for a 2D platformer.

Personally, I do also like the solution described as it feels like a nice, practical application of somewhat abstract topics which are commonly taught during graph theory sections of an undergraduate CS degree. It’s an abstraction which isn’t immediately obvious, but yet so useful and flexible to work with.

Further Reading

• A relevant Reddit thread.
• Stack Exchange answer which was one of the first resources I found on this topic.